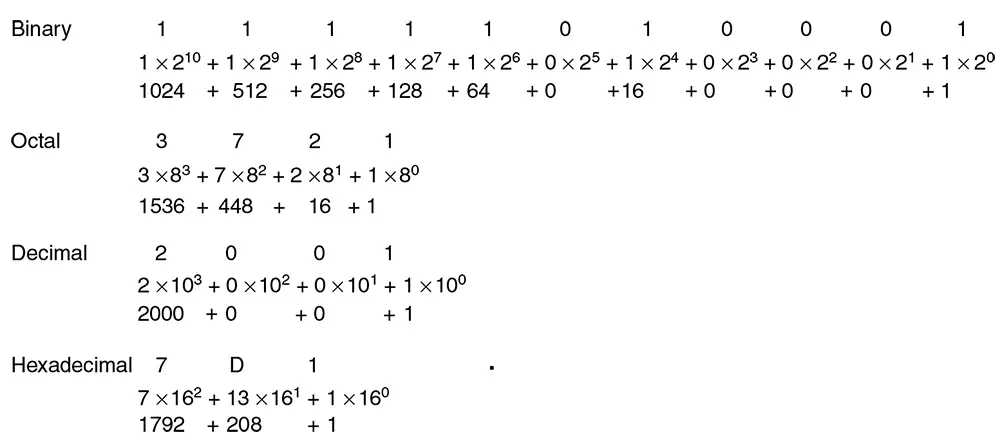1) Storing Numbers:
When storing numerical values, a digital computer leverages binary numbers to encode the information. Each digit within a binary number is referred to as a bit, the smallest unit of data in a computer. Multiple bits are combined to form larger units such as bytes (commonly 8 bits), kilobytes, megabytes, and so on.
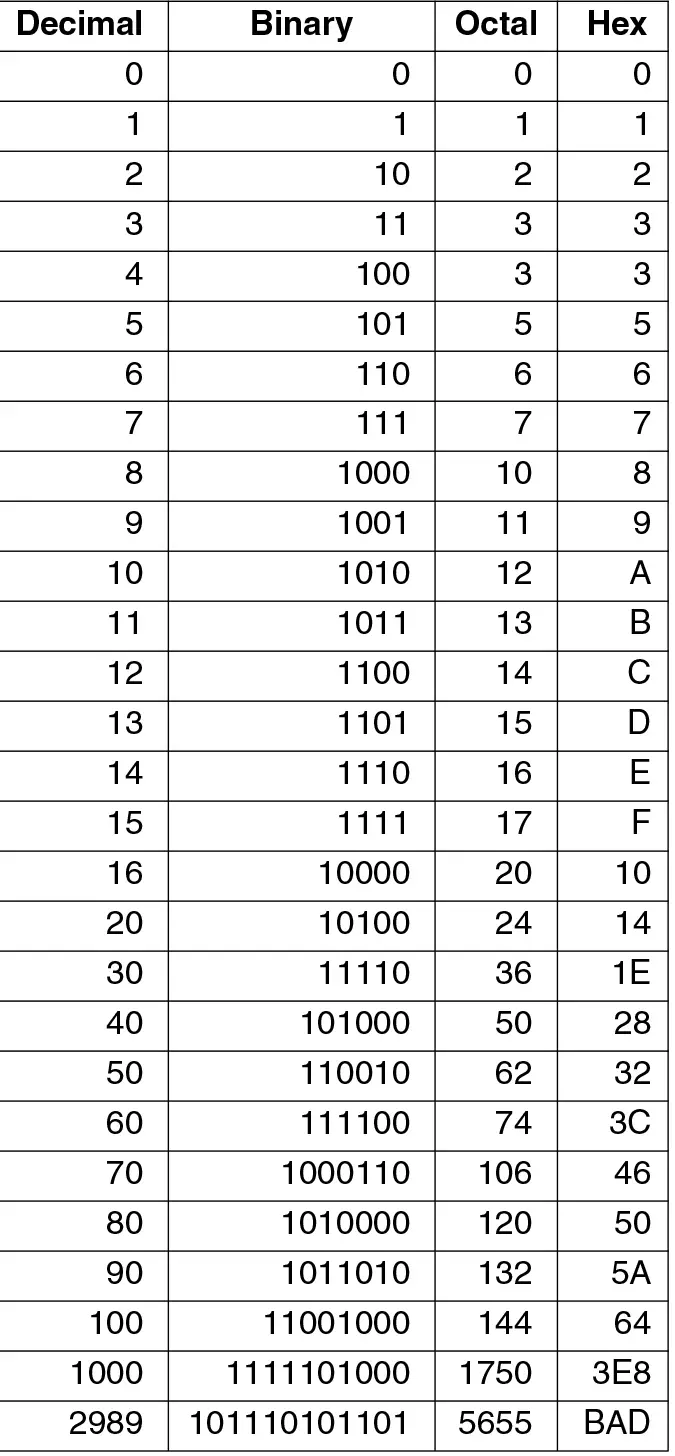
For example, the decimal number 5 is represented in binary as 101. This is calculated as (1 × 2^2) + (0 × 2^1) + (1 × 2^0), which equates to 4 + 0 + 1. The computer's memory stores this binary representation using transistors that are set to on or off states, corresponding to 1s and 0s, respectively.
Integers are typically stored in a fixed amount of space, such as 32 or 64 bits, with one bit sometimes used to represent the sign for signed numbers (positive or negative). Floating-point numbers, used to represent decimals and scientific notations, have a more complex binary representation that divides the bits between a sign, exponent, and fraction, following standards such as IEEE 754.
2) Storing Text:
For text storage, computers translate characters, such as letters, numbers, and symbols, into binary numbers using character encoding schemes. The most basic form of encoding is the American Standard Code for Information Interchange (ASCII), where each character is assigned a unique 7-bit binary number. For example, the capital letter 'A' is represented by the binary number 1000001 in ASCII.
More comprehensive encoding systems, like Unicode, use a variable number of bytes to accommodate a vast array of characters from multiple languages and symbols, supporting global communication and information exchange. A Unicode transformation format, such as UTF-8, represents each character with a unique binary sequence, which can vary in length to optimize storage space for common characters.
In both numbers and text representation, the binary system underlies the functioning of digital computers, enabling them to perform a wide range of operations by manipulating binary digits through their hardware circuits. This system of representation is efficient, reliable, and universally adopted in the design of computer architectures and digital communication systems.