| Lesson 6 | Two's complement representation |
| Objective | Represent negative numbers in two's complement representation. |
Two's Complement Representation
So far we have looked at how to represent non-negative numbers in binary form. To be more precise, we have really only looked at how
to represent non-negative integers in binary form. To represent both positive and negative integers in binary form we make use of the
leftmost bit as a sign bit. If the leftmost bit is 0, then the number is either zero or a positive integer. If the leftmost bit is 1,
then the number is negative. The use of a sign bit does not change the way in which non-negative integers are represented. For example, the decimal number 26 would still be represented in 8-bit binary form as
00011010. To represent negative integers in binary form you might suspect that we simply take the binary form for the corresponding positive number and change the sign bit from 0 to 1. It's not quite that straightforward.
Negative Integers Two's Complement Form
Negative integers are represented in what is called two's complement form.
To obtain the two's complement representation for a negative integer, we begin with the binary representation of the corresponding positive integer. Then we reverse each digit (the 1s become 0s and the 0s become 1s) and add 1 to the result.
As an example, let's determine the 8-bit binary form for the negative integer, -3. We start with the 8-bit binary form for 3, which is
As an example, let's determine the 8-bit binary form for the negative integer, -3. We start with the 8-bit binary form for 3, which is
00000011. Next we reverse each digit to produce 11111100. Finally, we add 1 as shown below to obtain
11111101. Determining the decimal number represented by a two's complement binary number involves the same steps. For example, suppose you have the 8-bit binary number 10110111. Because the leftmost bit is 1 you know this is a negative number, but which one? To find out you would reverse each digit to produce 01001000 and then add 1 to obtain 01001001. This is the 8-bit binary representation of the decimal number 73--thus our original binary number is the two's complement representation of the decimal number -73.
Negative Integers Representation
At this point you are probably wondering why negative integers are represented in this strange fashion.
The simple answer is that it makes arithmetic with signed integers easy for the computer to perform.
This is best illustrated with a simple example. Consider the sum of the integers 12 and -3.
To perform this addition, the computer would simply add the digits in the corresponding positions of the two 8-bit binary numbers, as shown below.
To perform this addition, the computer would simply add the digits in the corresponding positions of the two 8-bit binary numbers, as shown below.
00001100 11111101 ======== 00001001
In each column of the sum, when two 1s are added together the sum is 0 with a carry of 1, and when three 1s are added together the sum is 1 with a carry of 1. The carry after adding the digits in the leftmost position is discarded. The sum of the two numbers is
00001000. As expected, this is the 8-bit binary representation of the decimal number 9.
Radix Number Systems
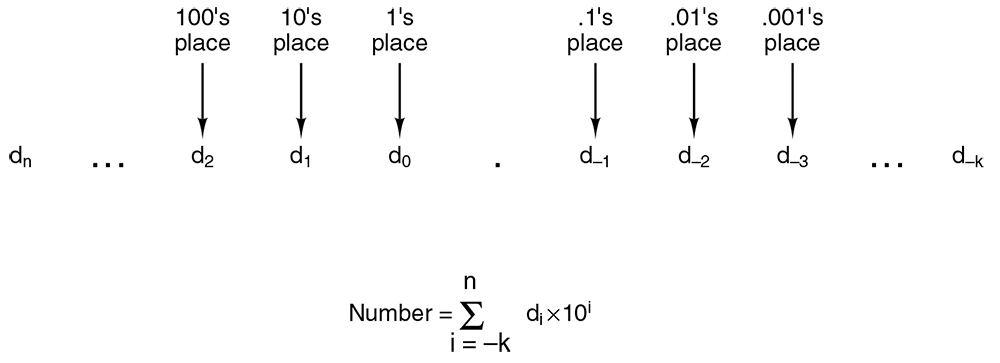
An ordinary decimal number with which everyone is familiar consists of a string of decimal digits and, possibly, a decimal point.
The general form and its usual interpretation are shown in Figure 3-5.1. The choice of 10 as the base for exponentiation, called the radix, is made because we are using decimal, or base 10, numbers. When dealing with computers, it is frequently convenient to use radices other than 10.
The most important radices are 2, 8, and 16. The number systems based on these radices are called binary, octal, and hexadecimal, respectively.
A radix k number system requires k different symbols to represent the digits 0 to k − 1. Decimal numbers are built up from the 10 decimal digits
0 1 2 3 4 5 6 7 8 9
In contrast, binary numbers do not use these ten digits. They are all constructed exclusively from the two binary digits.
0 1
Octal numbers are built up from the eight octal digits
0 1 2 3 4 5 6 7
0 1 2 3 4 5 6 7 8 9 A B C D E F
Two's complement: Binary representation for signed integers. Note that with 8 bits you can still represent 28 or 256 numbers, but when using the 8 bits to represent signed integers you can represent the integers -128 to 127 rather than the integers 0 to 255.
With n bits you can represent the signed integers
Here is a table showing the 8-bit two's complement binary numbers and their decimal equivalents.
-2n-1 to 2n-1 - 1.
Here is a table showing the 8-bit two's complement binary numbers and their decimal equivalents.
| Binary | Decimal |
|---|---|
0000000
|
0
|
You know know how signed integers are stored in a computer. Next we will examine how real numbers are stored.
Twos Complement Tepresentation - Quiz
Click the Quiz link below to test your understanding of two's complement representation.
Twos Complement Tepresentation - Quiz
Twos Complement Tepresentation - Quiz
Structured Computer Organization